반응형
https://www.acmicpc.net/problem/9735
9735번: 삼차 방정식 풀기
첫째 줄에 테스트 케이스의 개수 N (0 < N < 100)이 주어진다. 다음 N개 줄에는 삼차 방정식의 계수 A, B, C, D가 한 줄에 하나씩 주어진다.
www.acmicpc.net
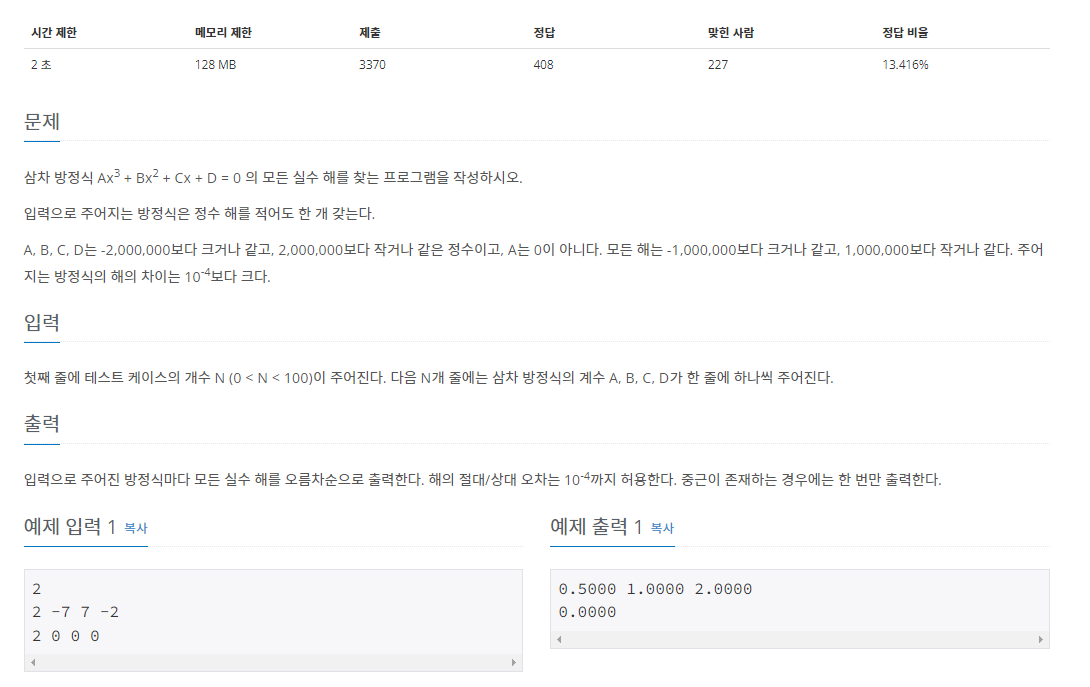
삼차방정식 문제
정수해 1개가 확정적으로 존재하는 삼차방정식의 해를 구해 출력해 보는 문제
삼차방정식의 수학적 개념을 이해해야 풀 수 있었다.
📌 문제 접근 포인트
1. 요구사항을 보면, x 중에 1개는 정수(α)로 주어짐을 알 수 있다. 즉, 정수의 숫자 1개를 이용해서 3차 방정식의 차원을 낮출 수 있다.
2. 정수값 1개 (α) 를 알고 있으면 삼차방정식은 (x-α)(a'x^2+b'x+c')의 꼴로 나타낼 수 있고, 나머지는 뒤의 2차 방정식을 풀면 총 해 3개를 얻을 수 있다. 이것을 이용해서 출력해 보자.
3. 정수 해를 구해주기 위해서 3차 방정식의 계수 d를 기준으로 생각해서 구하면 for 문을 이용해서 정수 해를 얻을 수 있다. 물론, 그냥 구할 수도 있지만 이렇게 if x %d를 이용해서 계수를 나눠주지 않을 경우 탐색 수가 늘어나서 시간이 더 오래 걸릴 수 있다. (물론 % d를 하지 않고, 3차 방정식 형태로 그대로 해도, if문의 계산을 반복하기 때문에 연산은 많아지지만 1초 안에 들어온다 )
4. 이렇게 구한 정수해 x를 이용해서, a, b, c 계수를 2차방정식으로 만들기 위해서 변형해 주자. 3차 방정식의 계수를 변경하면 a = 다항식, b = 1차식, c = 2차식의 해 형태로 만들 수 있다(모르겠으면 직접 인수분해를 한번 해보자)
5. 그럼 이제 2차 방정식의 계수를 다 구했으니, 판별식을 이용해 근이 1개, 2개, 3개 일 때를 각각 구해줄 수 있고, 오름차순으로 정렬 후에 출력을 하면 원하는 값을 얻을 수 있다.
⚙ 내가 푼 정답코드
def find():
for x in range(1,abs(d)+1):
if d % x == 0: # 삼차방정식 근의 관계에 의해 d는 무조건 x의 약수이므로
if a*x**2 + b*x + c + d//x == 0: # 다음 해를 만족하면 (양수 일 때)
return x # x 반환
elif -a*x**2 + b*x -c + d//x == 0: # 다음 해를 만족하면 (음수 일 때 x는 -니까)
return -x # -x 반환
return 0 # 없으면 해는 0
import sys
T = int(sys.stdin.readline())
for _ in range(T):
a, b, c, d = map(int, sys.stdin.readline().split())
x, result = find(), set()
a, b, c = a, a*x + b, a*x**2 + b*x + c # 정수 해 x를 아니, 이걸 토대로 2차 방정식으로 만들어주자
if b**2 - 4*a*c < 0: # 판별식 (근이 1개)
result.add(x) # x 하나 뿐
elif b**2 - 4*a*c == 0 : # 판별식 (근이 2개)
result.add(x) # 기본 해 x
result.add(-b / (2*a)) # 나머지 해 (1차 방정식의 해)
else : # 판별식 (근이 3개)
result.add(x) # 기본해 x
result.add((-b+(b**2 - 4*a*c)**(1/2))/(2*a)) # 나머지 해 1 (근의 공식)
result.add((-b-(b**2 - 4*a*c)**(1/2))/(2*a)) # 나머지 해 2 (근의 공식)
result = sorted(list(result)) #요구 조건에 따른 오름차순 정렬
# 밑에는 출력 요구조건
if len(result) == 3:
print(f'{result[0]:.4f} {result[1]:.4f} {result[2]:.4f}')
elif len(result) == 2:
print(f'{result[0]:.4f} {result[1]:.4f}')
else :
print(f'{result[0]:.4f}')반응형
'알고리즘 풀이 > 백준' 카테고리의 다른 글
| [백준 2740] 행렬 곱셈 (python) (0) | 2023.04.09 |
|---|---|
| [백준 15965] K번째 소수 (python) (0) | 2023.04.08 |
| [백준 4673] 셀프 넘버 (python) (0) | 2023.04.07 |
| [백준 11440] 피보나치 수의 제곱의 합 (python) (0) | 2023.04.07 |
| [백준 13977] 이항 계수와 쿼리 (python) (0) | 2023.04.07 |




댓글