https://www.acmicpc.net/problem/1492
1492번: 합
N과 K가 주어졌을 때, 1K + 2K + 3K + ... + NK를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
www.acmicpc.net
합 문제
1부터 N까지 각각 k제곱한 수들의 합을 구하는 문제
k의 수가 작아서 처리 시간이 오래 걸리지 않는 문제 이항계수, 분할정복, 다이나믹 프로그래밍 등의 개념을 적절하게 섞어서 해결 할 수 있는 문제로 수식을 연산하고 떠올리는 과정이 생각보다 어려워서, 쉽게 접근하기는 어려웠다.
오랜 시간 고민하고, 수식 변형해서 해낼 수 있던 문제!
📌 문제 접근 포인트
0. 제곱 수들의 합 아이디어에 대해서 참고하면 좋을 사이트
https://www.mathpages.com/home/kmath279/kmath279.htm
아래 내용이 이해가 안되면 위 사이트(특히 C가 나오는 적분 파트)를 먼저 보고 오는 것을 추천
1. 제곱 수들의 합을 구할 방법을 생각해보자.
아이디어를 떠올리기 위해서 먼저 k=1일때부터 생각해보자. 일반적으로 k = 1일때의 n까지의 합의 공식에 대해서는 이미 알고있다.

k=2일 때도 알고 있다.

그렇다면 공식으로 k에 대해서 공식을 만들 수 있지 않을까? 라는 생각으로 접근해보자.
합의 공식을 만드는 과정에 대해서 알고 있으면 접근 할 수 있다.
일반항을 만드려고 시도를 해보자. 기본적인 전개식은 아래와 같다

이 식을 이용해서 구해보자. 아래처럼 k+1항에 대해 계산을 할 수 있다.

그러면 오른쪽 최고차항을 우측으로 바꿔보자.

이 식을 n=1부터 대입해서 식을 만들어보자.
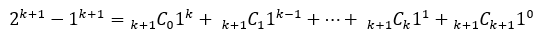
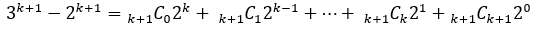
...

이제 각각 좌변 우변을 더해주면 제곱의 합에 대해 구할 수 있다.
좌변은 중간 항들은 계산해서 사라지고, 우측 항들은 각각 1~N까지 합한 항들이 된다.

즉, 이 식에 대해서 조금 더 이쁘게 정리해서 보면

다음처럼 식이 정리가 된다. 그렇다면 임시로 아래처럼 정의해주자.

그렇다면 우리가 필요한 이 f(m) 식은 다음처럼 계산된다.

이렇게 만들어낸 식을 이용해서 문제를 풀어보자.
2. 그렇다면 이 식을 어떻게 활용하면 좋을까?
이항계수를 계산하는 과정에서 필요한 항목은 팩토리얼과 제곱 수를 계산해줄 분할정복 등이 필요하다. 그렇다면 팩토리얼, 이항계수, 분할정복에 대한 함수를 각각 정의해서 사용해보자.
3. 이제 1번에서 구한 식을 토대로 다이나믹 프로그래밍을 구상해보자. 결국 위 식은 앞에서부터 누적돼서 계산이 되므로 다이나믹 프로그래밍을 활용할 수 있다.
4. 이제 각각의 식을 반복하고, 페르마의 소정리와 모듈로 연산을 넣어 결과값을 출력할 수 있도록 계산해주자.
✔ 개선 가능 포인트
1. 이항 계수를 구하는 과정이 복잡해져서 코드가 길어지고 연산 수가 많아졌는데(팩토리얼 활용 등) 굳이 사용하지 않고 이항 계수를 어렵지 않게 구할 수 있는 '파스칼의 삼각형' 개념을 이용했으면 더 짧아졌을 것이다
2. 내부 for문에 대해서 따로 t로 구현을 하고 빼주었는데, 굳이 t로 추가 변수선언 하지 않고 x에 직접적으로 -=를 이용해서 계산하면 변수, 코드 수도 줄일 수 있었다
3. dp의 다음항을 계산하는 과정에서 페르마의 소정리를 활용했는데, 생각해보니 아래 k+1Ck는 결국 그냥 k+1인데 추가로 이항 계수 구현을 해줘서 괜히 추가 연산이 들어간 점 등을 개선 할수 있을 것 같다.
⚙ 내가 푼 정답 코드
def factor(n): # 이항계수 계산용 팩토리얼
result = 1
for i in range(2,n+1):
result *= i
return result
def square(a,n):
if n == 1:
return a
x = square(a,n//2)
if n % 2 == 0 :
return x*x % mod
else :
return x*x*a %mod
def combin(n,k): # 조합 갯수 결과 (페르마의 소정리)
a = factor(n) % mod
b = square(factor(k) * factor(n-k), mod-2) % mod
return a*b % mod
import sys
N, p = map(int,sys.stdin.readline().split())
mod = 10**9+7
dp = [0] * (p + 1)
dp[0] = N
for i in range(1, p+1):
t = 0
x = (N+1) **(i+1) - 1 # 제곱의 합 구하는 공식
for j in range(i):
t += combin(i+1,j) * dp[j] # 이항계수 (i+1, j) * 이전 공식 사용한 것들의 합
y = combin(i+1,i) # 각 계수
# 다음 dp는 x-y를 (i+1,i)의 이항계수로 나눈 값
dp[i] = (((x-t) % mod) * (square(y,mod-2) % mod)) % mod #(제곱의 합- 계수 합) * 이항 계수의 역수(페르마의 소정리)
print(dp[p] % mod)
'알고리즘 풀이 > 백준' 카테고리의 다른 글
| [백준 10942] 팰린드롬? (python) (0) | 2023.04.10 |
|---|---|
| [백준 25974] 거듭제곱의 합1 (python) (0) | 2023.04.09 |
| [백준 10830] 행렬 제곱 (python) (0) | 2023.04.09 |
| [백준 2740] 행렬 곱셈 (python) (0) | 2023.04.09 |
| [백준 15965] K번째 소수 (python) (0) | 2023.04.08 |




댓글