반응형
정의
- 무식하게 진행 한다는 의미로 brute force 알고리즘이라 불리며 가능한 모든 경우의 수를 모두 탐색하기에 완전 탐색 알고리즘이라고도 불린다.
- 일반적으로 문제 해결을 위해서 모든 자료를 탐색해야 하기에 특정 구조를 전체적으로 탐색할 수 있는 방법 요구
- 선형 구조로 탐색하는 순차 탐색, 비선형 구조로 탐색하는 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 가장 기본적인 방법 → 브루트 포스와 가장 관련이 깊은 방법은 BFS
- 비밀번호 자물쇠를 생각하면 이해하기 쉽다 (단순히 무식하게 4자리 자물쇠를 확인하더라도 총 10^4번의 확인이 필요하다)
장점
- 알고리즘 설계와 구현이 매우 쉽다.
- 복잡한 알고리즘 없이 빠르게 구현이 가능하다
단점
- 알고리즘의 실행 시간이 매우 오래 걸린다
- 메모리 효율면에서 매우 비효율적이다 (단순하게 4자리숫자 핸드폰 암호를 푸는 코드의 시간 복잡도 : O(n^4)
순차탐색의 과정
1. 문제에서 주어진 자료를 선형 구조로 바꾼다.
2. 구조화 된 자료들을 구조에 맞는 방법으로 해를 구할 때 까지 탐색한다.
3. 탐색한 해를 주어진 문제의 출력 형식에 맞게 정리한다.
반응형
너비 우선 탐색(BFS)
루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
- 주로 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 사용
- ex) 지구상에 존재하는 모든 친구 관계를 표현 후 A와 B 사이에 존재하는 경로를 찾는 경우
- 깊이 우선탐색의 경우 모든 친구 관계를 다 살펴봐야함 → 너비 우선 탐색의 경우 A와 가까운 관계부터 탐색
- 직관적이지 않은 면이 있음
- BFS는 재귀적으로 동작 x
- 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다. (검사하지 않을 경우 무한 루프에 빠질 수 있음)
- 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(queue)를 주로 사용
- 시간 복잡도
- 인접 리스트로 표현된 그래프 : O(N+E)
- 인접 행렬로 표현된 그래프 : O(N^2)
장점
- 모든 경로를 탐색하기에 여러 해가 있을 경우에도 최단 경로임을 보장
- 최단 경로가 존재하면 깊이가 무한정 깊어진다고 해도 답을 찾기 가능
- 노드의 수가 적고, 깊이가 얕은 해가 존재할 때 유리
단점
- 노드의 수가 많을수록 탐색 가지가 급격히 증가함에 따라 보다 많은 메모리가 필요함
- 노드의 수가 많을수록 탐색 가지가 급격히 증가함에 따라 보다 많은 메모리가 필요함

from collections import deque
graph = [[], [2, 3], [4, 5], [6], [2, 5], [2, 4], [3, 7], [6]]
visited = [False] * 8
def bfs(v):
q = deque()
q.append(v)
# 아직 방문해야 하는 노드가 있다면
while q:
# 큐에서 노드를 꺼내서 x에 저장
x = q.popleft()
print(x, end=' ')
# 그래프를 탐색하다가 방문하지 않은 노드가 있다면
for i in graph[x]:
if not visited[i]:
# 큐에 방문하라고 삽입하고 방문 처리
q.append(i)
visited[i] = True
bfs(1)
깊이 우선 탐색 알고리즘 (DFS)
그래프의 깊은 부분을 우선적으로 탐색하는 알고리즘
- LIFO 방식을 따르는 스택을 통해 구현
- 재귀 함수를 사용하여 구현 할 수도 있음
장점
- 단지 현 경로상의 노드들만 기억하면 되므로 저장 공간의 수요가 비교적 적음
- 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있음
단점
- 해가 없는 경로에 깊이 빠질 가능성이 있음
- 얻어진 해가 최단 경로가 된다는 보장이 없음 (목표에 이르는 경로가 다수인 문제에 대해 DFS는 해에 다다르면 탐색을 끝내므로)
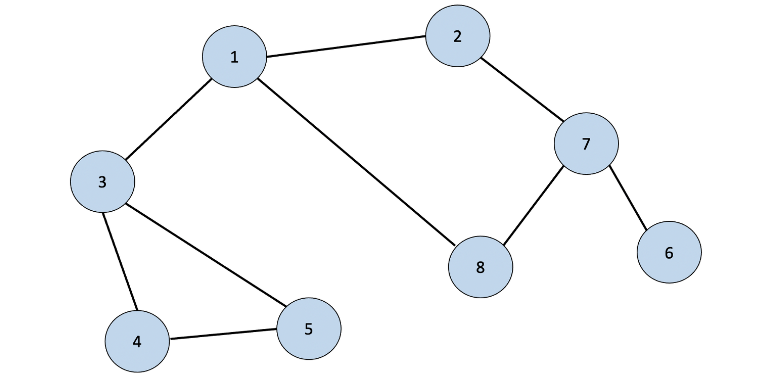
# 스택을 사용하는 방식
graph = [ [], [2, 3, 8], [1, 7], [1, 4, 5], [3,5], [3, 4], [7], [2, 6, 8], [1, 7]
visited = [False] * len(graph)
def dfs(graph, v, vsisted):
visited[v] = True
print(v, end=' ')
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
dfs(graph, 1, visited)
# 재귀를 사용하는 방식
def dfs_recursive(graph, start, visited = []):
visited.append(start)
for node in graph[start]:
if node not in visited:
dfs_recursive(graph, node, visited)
return visited
반응형
'언어별 개념 정리 > Python' 카테고리의 다른 글
| [파이썬] 부분집합을 구하는 방법 (0) | 2023.02.12 |
|---|---|
| [파이썬] 정렬 알고리즘 - 버블 정렬 & 카운팅 정렬 (0) | 2023.02.12 |
| [파이썬] 스택(Stack) 알고리즘 정리 - 계산기 구현하기 (0) | 2023.02.08 |
| [파이썬] 문자열(String) 알고리즘 정리 - 보이어 무어(Boyer-moore) 알고리즘 (0) | 2023.02.07 |
| [파이썬] 알고리즘 풀이에 자주 사용되는 python 함수 및 알고리즘 기술 정리하기 (0) | 2023.02.05 |




댓글