반응형
너비 우선 탐색(Breadth First Search, BFS)
루트노드(혹은 다른 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
- 시작 정점으로부터 가까운 정점을 방문해나가 가장 멀리 떨어진 정점을 나중에 방문하는 순회 방법
- 말그대로 넓게 탐색하는 방법 (방문한 노드를 기준으로 주변을 탐색해나가므로)
- 깊이 우선 탐색보다 조금 더 복잡함
특징
- 거리에 따라 단계별로 탐색하므로 직관적이지 않은 면이 있음
- 그래프 탐색의 경우 어떤 노드를 방문했는지 반드시 검사해야 함 → 그렇지 않을 경우 무한 루프에 빠질 위험 있음
- 재귀적으로 동작하지 않음
- 방문한 노드를 차례로 저장한 후 꺼내는 큐(Queue)를 사용(선입선출의 원칙)
- 시간 복잡도는 O(N)의 시간 소요 (단, 실제 수행 시간은 DFS > BFS)
방문 원리 순서
- 시작 노드인 1을 큐에 삽입하고 방문 처리

2. 큐에서 1을 꺼내고, 인접한 노드인 2, 3, 4를 큐에 삽입
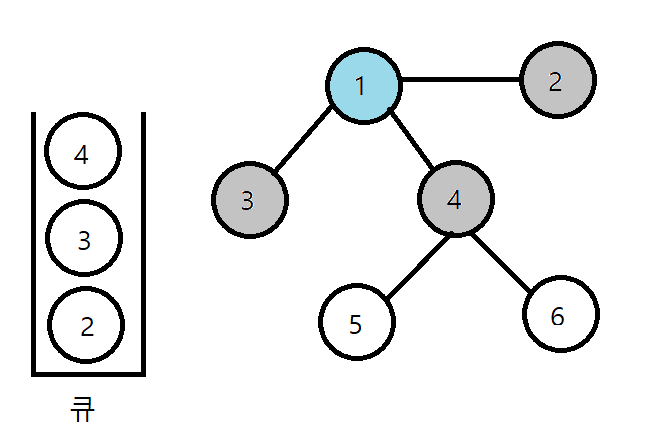
3. 큐에서 2를 꺼내고 방문 처리

4. 큐에서 3을 꺼내고 방문 처리
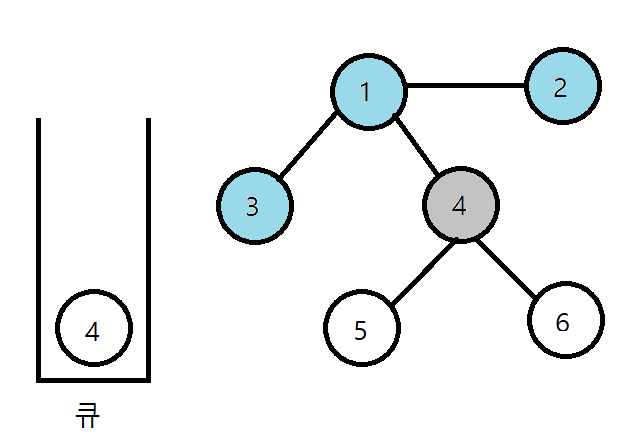
5. 큐에서 4를 꺼내고 방문처리 후 인접 노드인 5, 6을 큐에 삽입
반응형

6. 큐에서 5를 꺼내고 방문처리

7. 최종적으로 6까지 방문처리
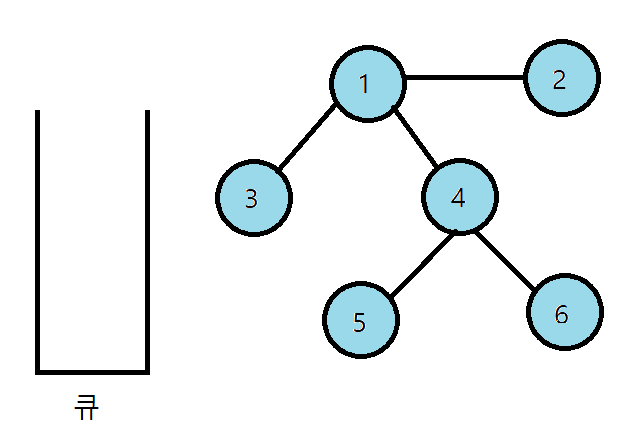
큐에 삽입된 순서는 1 > 2> 3> 4> 5 > 6
이럴때 사용
- 주로 최단 경로 문제 해결에 사용(두 정점간의 최단 경로를 찾는다거나..)
- cheney's algorithm나 copying garbage collection 등을 해결하는데 사용
- https://en.wikipedia.org/wiki/Cheney's_algorithm (위키피디아)
- cheney’s algorithm의 Article 부분 맨 마지막 문장에 this is known as a breadth-first list copying garbage collection scheme이라 쓰여있는것을 볼 수 있음
일반적인 BFS 소스코드
def BFS(graph, S): # BFS 정의
visited = [False]*(len(graph)+1) # 방문 처리를 위해 생성
queue = []
queue.append(S)
visited[S] = True # 현재 노드 방문처리
while queue :
a = queue.pop(0) #큐에 순차적으로 삽입
print(a, end = ' ')
for i in graph[a]: #방문하지 않은 인접 노드들을 큐에 삽입
if not visited[i] :
queue.append(i)
visited[a] = True
graph = [[],[2,3,4],[],[],[5,6],[],[]]
BFS(graph,1)
# 출력결과 : 1, 2, 3, 4, 5, 6
방문한 노드까지의 길이를 확인하는 소스코드(예시 미로)
#시작 지점이 2, 종점이 3인 미로를 종점까지의 거리 탐색하는 코드
def bfs(a, b):
visited = [[0] * N for _ in range(N)]
move = [[1, 0], [-1, 0], [0, 1], [0, -1]] # 상하좌우
queue = []
queue.append([a, b]) # 큐에 초기값 지정
visited[a][b] = 1 # 초기값 1
while queue:
y, x = queue.pop(0)
if maze[y][x] == 3:
return visited[y][x] - 2 # 도착지점 기준 시작값 1과 끝값 1을 뺴줘야함
for dy, dx in move:
ny, nx = y + dy, x + dx
# 범위 밖을 벗어나지 않으면서 1이 아니고, 방문하지 않았을 경우
if 0 <= ny < N and 0 <= nx < N and maze[ny][nx] != 1 and visited[ny][nx] == 0:
visited[ny][nx] = visited[y][x] + 1
queue.append([ny, nx])
return 0
N = 5
maze = [[1,1,2,1,1],[1,1,0,1,1],[1,1,0,1,1],[1,1,0,1,1],[1,1,0,0,3]]
print(bfs(0,2))
# 출력 결과 6반응형
'언어별 개념 정리 > Python' 카테고리의 다른 글
| [파이썬] 알고리즘 - 트리 순회 (전위, 중위, 후위) (python) (0) | 2023.02.27 |
|---|---|
| [파이썬] 탐색 알고리즘 정리 - 깊이 우선 탐색(DFS) (python) (0) | 2023.02.26 |
| 소수 판별 알고리즘 - 에라토스테네스의 체 (0) | 2023.02.21 |
| [파이썬] 메모이제이션과 동적 프로그래밍 (0) | 2023.02.19 |
| [파이썬] 큐(Queue) 자료구조 정리 (0) | 2023.02.15 |




댓글