반응형
트리(Tree)
트리는 노드(node)와 노드들을 연결하는 에지(edge)로 이루어진 자료 구조
특징
- 각 노드는 하나의 부모 노드와 여러 개의 자식 노드를 가질 수 있음.
- 트리는 그래프의 한 종류로, 루트(root) 노드에서 시작하여 모든 노드를 방문할 수 있는 구조.
이진 트리(Binary Tree)
이진 트리는 각 노드가 최대 두 개의 자식 노드를 갖는 트리, 자료 구조에서 가장 널리 쓰이는 구조
참고사항
트리는 계층적인 구조를 나타내기 때문에, 운영 체제에서 디렉터리 구조, 인터넷에서의 사이트 맵, 컴파일러에서의 구문 분석 트리 등에 적용
트리 순회(Tree Traversal)
트리 순회는 트리의 모든 노드를 방문하는 방법
전위 순회(preorder traversal)
부모노드 → 왼쪽 자식 노드 → 오른쪽 자식 노드의 순서로 방문
순회 과정
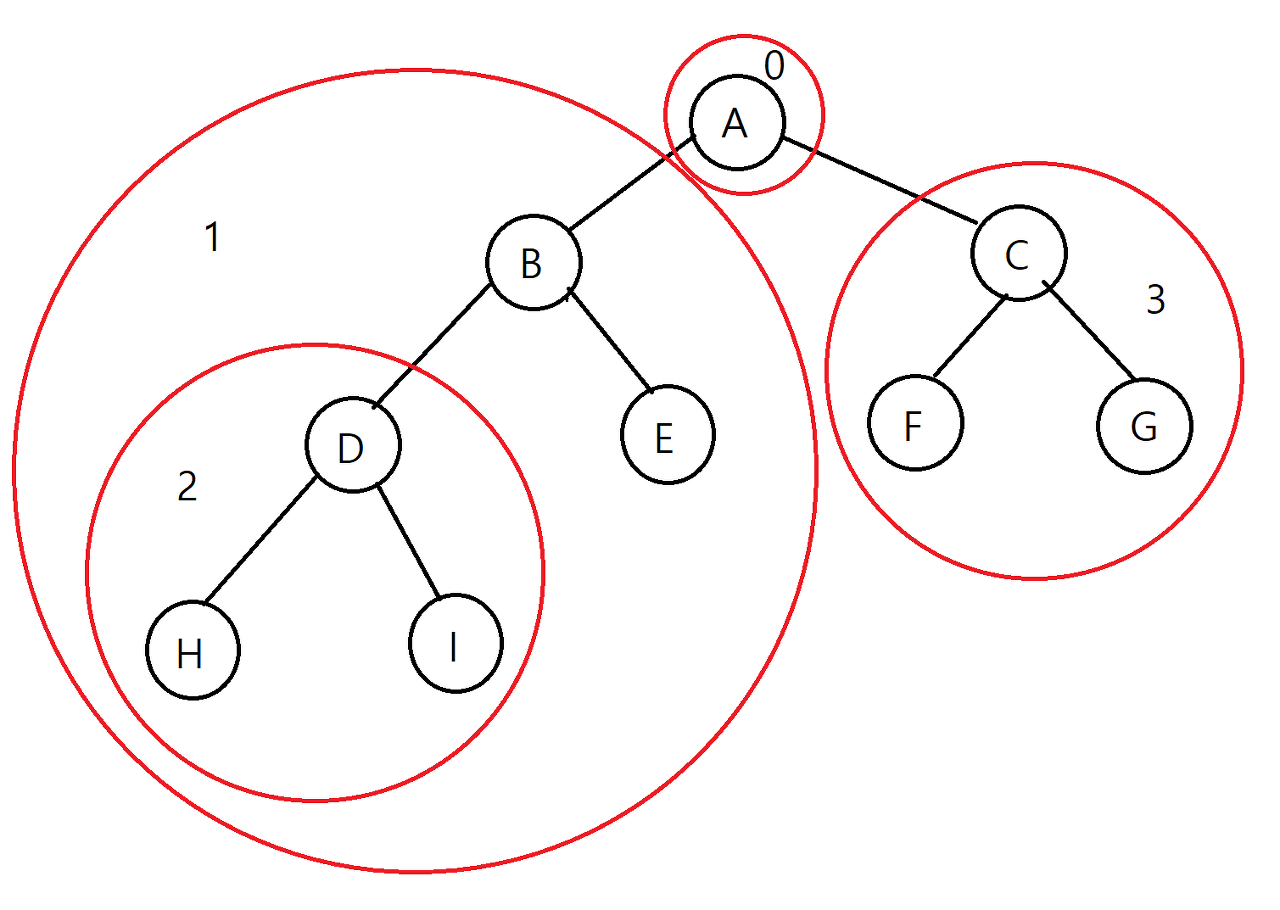
- 전위 순회로 순차적으로 순회 할 경우 탐색 순서는 0 → 1 → 3의 순서로 탐색
- 여기서 1의 왼쪽 서브트리에 2가 있으므로 0 → 1 → 2 → 3 으로 탐색
- 노드 순서는 A → B → D → H → I → E → C → F → G
코드 구현(위 그림 예시)
# 전위 순회 탐색 코드
def preorder(a):
if a <= N:
print(tree[a], end=' ')
preorder(a*2)
preorder(a*2 + 1)
N = 9
tree = [0, 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H','I']
print(tree)
preorder(1)
#출력 A B D H I E C F G
중위 순회(inorder traversal)
왼쪽 자식노드 → 부모 노드 → 오른쪽 자식 노드 순으로 방문
순회 과정

- 중위 순회로 순차적으로 순회 할 경우 탐색 순서는 1 → 0 →3의 순서로 탐색
- 여기서 1의 왼쪽 서브트리에 2가 있으므로 2 → 1 → 0 → 3 →으로 탐색
- 노드 순서는 H → D → I → B → E → A → F → C → G
코드 구현(위 그림 예시)
# 중위 순회 탐색 코드
def inorder(a):
if a <= N:
inorder(a*2)
print(tree[a], end=' ')
inorder(a*2 + 1)
N = 9
tree = [0, 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H','I']
print(tree)
inorder(1)
#출력 H D I B E A F C G
반응형
후위 순회(postorder traversal)
왼쪽 자식노드 → 오른쪽 자식 노드 → 부모 노드 순으로 방문
순회 과정

- 후위 순회로 순차적으로 순회 할 경우 탐색 순서는 1 → 3 → 0
- 여기서 1의 왼쪽 서브트리에 2가 있으므로 2 → 1 → 3→ 0으로 탐색
- 노드 순서는 H → I → D → E → B → F → G → C → A
코드 구현(위 그림 예시)
# 후위 순회 탐색 코드
def postorder(a):
if a <= N:
postorder(a*2)
postorder(a*2 + 1)
print(tree[a], end=' ')
N = 9
tree = [0, 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H','I']
print(tree)
postorder(1)
#출력 H I D E B F G C A
개인의견
순회 과정의 경우 재귀 함수 사이에 print 위치만 다르게 찍으면 되는 것을 알 수 있으니 코드 1개만 외우면 된다
반응형
'언어별 개념 정리 > Python' 카테고리의 다른 글
| [Python] 알고리즘 풀이 시 유용한 함수 사용 팁 (map, join 등) (0) | 2023.04.29 |
|---|---|
| [파이썬] 탐색 알고리즘 정리 - 백트래킹 (1) | 2023.03.12 |
| [파이썬] 탐색 알고리즘 정리 - 깊이 우선 탐색(DFS) (python) (0) | 2023.02.26 |
| [파이썬] 탐색 알고리즘 정리 - 너비 우선 탐색(BFS) (python) (0) | 2023.02.22 |
| 소수 판별 알고리즘 - 에라토스테네스의 체 (0) | 2023.02.21 |




댓글