자격증 준비하면서 내가 이해하기 편하게, 다시 보기 좋게 정리하는 빅데이터 분석기사의 내용 (자격증 상세 내용은 아래)
https://www.dataq.or.kr/www/sub/a_07.do
데이터자격시험
대용량의 데이터 집합으로부터 유용한 정보를 찾고 결과를 예측하기 위해 목적에 따라 분석기술과 방법론을 기반으로 정형/비정형 대용량 데이터를 구축, 탐색, 분석하고 시각화를 수행하는 업
www.dataq.or.kr
2과목인 빅데이터 분석 기획을 정리한 내용
평균
- 산술 평균 : 산술 평균은 자료를 모두 더한 후 자료 개수로 나눈 값으로 전부 같은 가중치를 두며 이상값에 민감
- 모평균 : 모집단의 데이터가 N개일 때 X1, X2, … , XN에 대한 평균
- 표본평균 : 표본의 데이터가 n개일 때 X1, X2, …, Xn에 대한 평균
- 기하 평균 : 숫자들을 모두 곱한 후 거듭제곱근을 취해서 얻은 평균. 성장률, 백분율과 같이 자료가 비율이나 배수와 같이 곱의 관계 일 때 사용
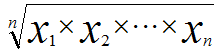
- 조화 평균 : 자료들의 역수에 대해 산술 평균을 구한 후 그것을 역수로 취한 평균. 속도의 평균, 여러 곳의 평균 성장률과 같은 곳에 사용
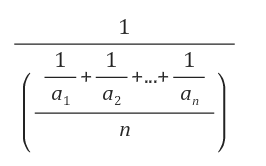
중위수(중윗값)
- 모든 데이터값을 오름차순으로 순서대로 배열하였을 때 중앙에 위치한 데이터값
- 이상치에 영향받지 않음
- ex) 45, 100, 70, 85, 70, 65, 75, 90의 데이터가 있을 경우 중위수는 d = (8+1)/2 = 4.5번째 이므로 4번째 값인 85, 5번째 값인 70의 평균인 77.5가 중위수
최빈수
- 데이터값 중에서 빈도수가 가장 높은 데이터값
- ex) 45, 100, 70, 85, 70, 65, 75, 90의 데이터가 있을 경우 가장 많이 나온 최빈수는 70
※ 기출문제

산술평균, 기하평균, 최빈값은 중심화 경향 기초통계량이고 범위는 산포도(퍼짐 정도)에 대한 기초적 통계량이다. (답 : 4)
사분위수
- 제1 사분위수 : 데이터를 오름차순 했을 때 첫 번째 사등분점
- 제2 사분위수(중위수) :데이터 오름차순을 했을 때 두 번째 사등분점
- 제3 사분위수 : 데이터를 오름차순을 했을 때 세 번째 사등분점
분산
평균으로부터 얼마나 떨어져 있는지를 나타내는 값
- 모분산

- 표본분산

표준편차
분산에 양의 제곱근을 취한 값
- 모 표준편차

- 표본 표준편차
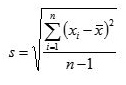
IQR(사분 범위, 사분위수)
제3 사분위수와 제1 사분위수의 차이 값
사분편차
제3 사분위수와 제1 사분위수 차이인 IQR의 절반 값
※ 기출문제

Q1 = (11+1) × (25/100) = 3 이므로 3번째 수치인 12이고, Q3=(11+1)(75/100) = 9이므로 9번째 수치인 19이다. 따라서 사분위편차는 19-12 = 7이 된다.(답 : 2)
변동계수(CV)
변동계수는 표주편차를 평균으로 나눈 값으로 측정 단위가 서로 다른 자료의 흩어진 정도를 상대적으로 비교할 때 사용
첨도(Kurtosis)

왜도(Skewness)
데이터 분포의 기울어진 정도를 설명하는 통계량
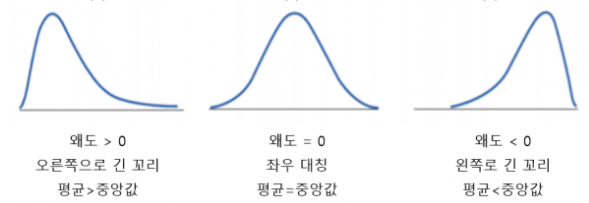
공분산(Covariance)
2개의 변수 사이의 관련성을 나타내는 통계량 (상관관계의 상승 혹은 하강하는 경향 이해 가능)
- Cov > 0 일 경우 2개의 변수 중 하나의 값이 상승하는 경향을 보일 때, 다른 값도 상승하는 경향을 보인다면 공분산의 값은 양수가 됨
- Cov < 0 일 경우 2개의 변수 중 하나의 값이 하강하는 경향을 보일 때, 다른 값도 상승하는 경향을 보인다면 공분산의 값은 음수가 됨
- 모공분산
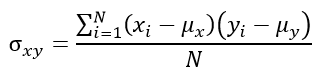
- 표본공분산
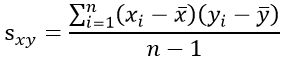
상관관계
두 변수 사이에 어떤 선형적 또는 비선형적 관계가 있는지를 분석하는 방법(인과관계는 알 수 없음)
- 변수 개수에 따른 분류
- 단순 상관 분석 : 두 개의 변수 사이의 상관성 분석
- 다중 상관 분석 : 세 개 이상의 변수 사이의 상관성 분석
- 변수 속성에 따른 분류
- 수치적 데이터 : 등간 척도, 비율 척도, 수치로 표현 가능한 데이터 변수 등 (피어슨 상관계수 분석)
- 순서적 데이터 : 범주형 데이터 중에서 순서적 데이터에 해당. 해데이터의 순서에 의미를 부여한 데이터 변수(스피어만 순위상관계수)
- 명목적 데이터 : 범주형 데이터 중에서 명목척도에 해당. 숫자나 기호를 할당한 데이터변수(카이제곱 검정 교차 분석)
※ 기출문제

동변량성 : X의 값에 관계없이 Y의 흩어진 정도가 같은 것을 의미한다. (답 : 2)
상관계수
두 변수 사이의 연관성을 수치상으로 객관화하여 두 변수 사이의 방향성과 강도를 표현하는 방법
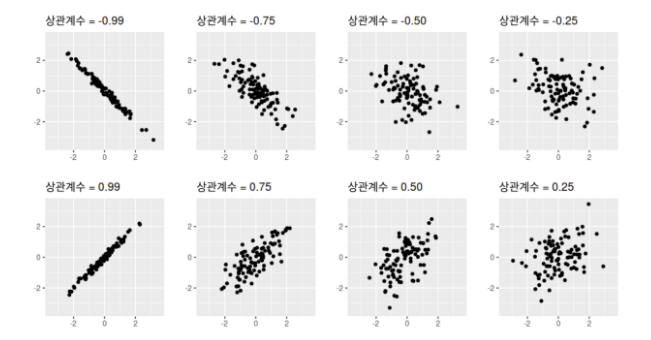
수치적 데이터의 상관계수
표본집단 피어슨 상관 계수
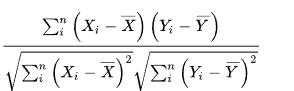
모집단 피어슨 상관 계수는 각각 X모집단이 평균, Y 모집단의 평균으로 대입하면 구할 수 있음
ex) 피어슨 상관계수 예시 모집단 X가 1,2,3 모집단 Y가 2,4,6 이면 X의 평균 μx = 2Y의 평균 μy = 4 이므로 위 공식에 의해
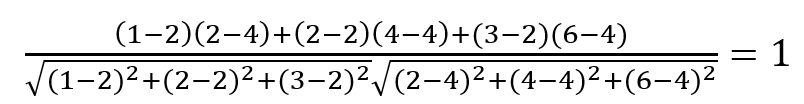
피어슨 상관계수는 1이므로 강한 양의 상관관계를 갖는다.
※ 기출문제

피어슨 상관계수는 두 변수 X와 Y 간의 선형 상관관계를 계량화한 수치이다. (답 : 3)
순서적 데이터의 상관계수
스피어만 순위 상관계수

n에 모집단 or 표본집단 데이터만 넣으면 원하는 집단 데이터를 구할 수 있음
ex) 스피어만 순위 상관계수 예시
모집단 X가 1,2,3 모집단 Y가 2,4,6 이면 모집단 R은 1,2,3 모집단 S는 1,2,3이다. 이때 R의 평균 μR = 2, S의 평균 μS = 2이므로
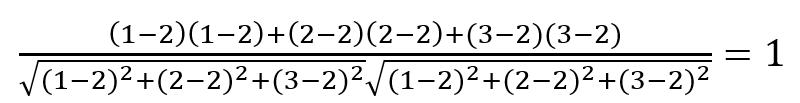
모집단 스피어만 상관계수는 1이므로 강한 양의 상관관계를 갖는다.
표본추출(Sampling)
모집단 일부를 일정한 방법에 따라 표본으로 선택하는 과정
- 전수 조사 : 모집단으로부터 직접적으로 정보를 입수하는 방법
- 모집단 ↓, 분산 ↑, 시간 비용이 충분하고, 대상이 비파괴성일 때 사용
- 표본 조사 : 표본집단으로부터 간접적으로 정보를 입수하는 방법
- 모집단 ↑, 분산 ↓, 시간 비용이 부족하고, 대상이 파괴성일 때 사용
표본추출 종류
- 단순 무작위 추출
- 모집단에서 정해진 규칙 없이 표본을 추출하는 방식
- 표본의 크기가 커질수록 정확도가 높아지고, 추정값이 모수에 근접하므로 추정 값의 분산이 줄어듦
- 계통 추출
- 모집단을 일정한 간격으로 추출하는 방식
- 층화 추출
- 모집단을 여러 계층으로 나누고, 계층별로 무작위 추출을 수행하는 방식
- 층 내는 동질적이고, 층간은 이질적
- 군집 추출
- 모집단을 여러 군집으로 나누고, 일부 군집의 전체를 추출하는 방식
- 집단 내부는 이질적이고, 집단 외부는 동질적
※ 기출문제

보기는 층화추출에 대한 설명이다. (답 : 3)

추출 모집단에 대해 사전지식이 많지 않은 경우 시행하는 것은 단순 무작위추출방법의 특징이다. (답 : 1)
확률분포
- 확률
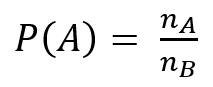
- 교사건

- 조건부 확률
- 어떤 사건이 일어난다는 조건에서 다른 사건이 일어날 확률
- 사건 B가 조건으로 일어났을 때, 사건 A의 조건부 확률
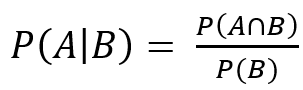
※ 기출문제

이론적으로 값은 통계적 확률 시행을 무한 번 반복시행하면 수학적 확률 값으로 수렴한다. (답 : 3)
전 확률의 정리
나중에 주어지는 사건 A의 확률을 구할 때 그 사건의 원인을 여러 가지로 나누어서, 각 원인에 대한 조건부 확률 P(A|Bi)와 그 원인이 되는 확률 P(Bi)의 곱에 의한 가중합으로 구할 수 있다는 법칙

베이즈 정리
어떤 사건에 대해 관측 전 원인에 대한 가능성과 관측 후의 원인 가능성 사이의 관계를 설명하는 확률 이론

ex) A 공장 부품의 생산율 50%, 불량률 1% , B 공장의 생산율 30%, 불량률 2%, C 공장의 생산율 20%, 불량률 3% 일 때 C공장에서 생산된 부품일 확률
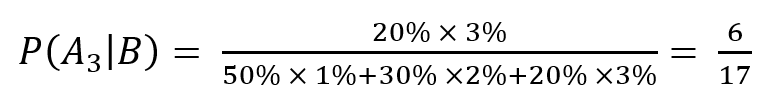
기댓값(E)
- 확률 변수의 값에 해당하는 확률을 곱하여 모두 더한 값
- 확률 변수의 평균과 같으며, E(X)로 표시
- 확률분포에서 평균적으로 기대할 수 있는 값이고, 해당 확률분포의 중심 위치를 설명해 주는 값
- 이산확률변수
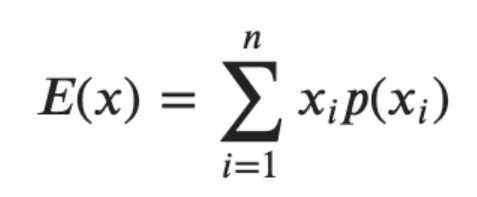
- 연속확률변수
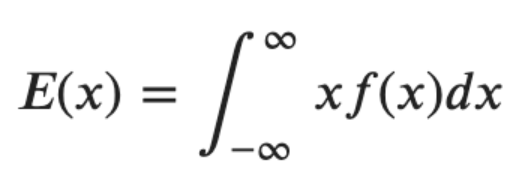
- 다음의 공식들을 모두 만족하는 특징 → E(a) = a / E(aX) = aE(X) / E(aX+b) = aE(X)+b / E(X±Y) = E(X)±E(Y) / E(XY)=E(X)E(Y) (단, X, Y가 독립)
분산
- 평균으로부터 얼마나 떨어져 있는지를 나타내는 값
- V(X) 또는 Var(X)로 표시
- 이산확률변수
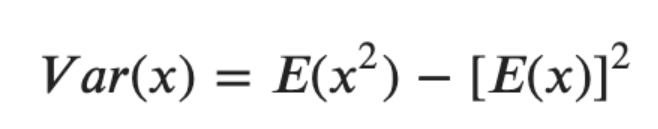
- 연속확률변수
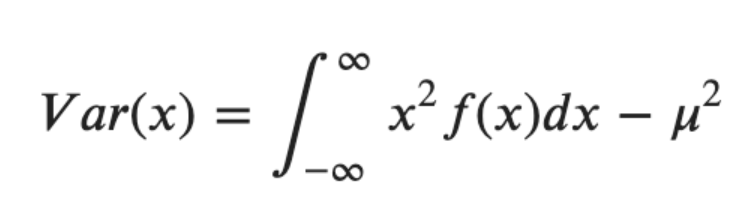
- 두 개의 확률 변수의 공분산
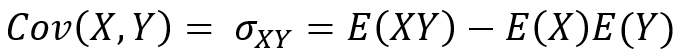
체비셰프 정리
- 임의의 양수 k에 대하여 확률변수가 평균으로부터 k배의 표준 편차 범위 내에 있을 확률에 대한 예측값을 보수적으로 제공하는 정리

- 관측값들의 분포에 상관없이 성립하나, 확률에 대한 하한값만을 제공
확률 분포
- 포아송 분포
이산형 확률 분포 중 주어진 시간 또는 영역에서 어떤 사건의 발생 횟수를 나타내는 확률 분포
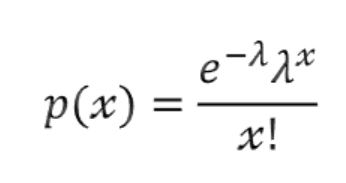
기댓값 E(X) = λ, 분산 V(X) = λ1
예시
ex) 나사 100개를 기준으로 1개가 불량일 때 나사 200개 중에서 불량이 1개 이하일 확률은?
100개 기준 1개 불량이면 200개는 2개 불량이므로 λ =2
불량이 1개 이하일 확률은 불량이 0개(n=0) 일 때 확률과 불량 1개(n=1) 일 때 확률을 합친 값
→ 포아송 계산에 의해 P(0) = e^-2, p(1)=2e^-2이므로 p = p(0) + p(1) = 3e^-2
- 베르누이 분포
특정 실험의 결과가 성공 또는 실패로 두 가지의 결과 중 하나를 얻는 확률분포
P=p, 기댓값 E(X) = p, V(X)= p(1-p) - 이항분포
n번 시행 중에 각 시행의 확률이 p 일 때, k번 성공할 확률

예시
기댓값 E(X) = np, 분산 V(X) = np(1-p) (단, n=k=1 이면 베르누이 시행)
ex) 동전 2번 던져서 1번이 앞면이 나올 확률은?
앞면(p=0.5)이 2번(n=2) 시행 중 1번(x=1) 성공할 확률
→ P=₂C₁*(0.5)(0.5) = 0.5
※ 기출문제

포아송 분포는 이산확률분포이고 나머지는 연속확률분포이다. (답 : 1)

포아송 분포 : 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산확률분포이다. (답 : 4)
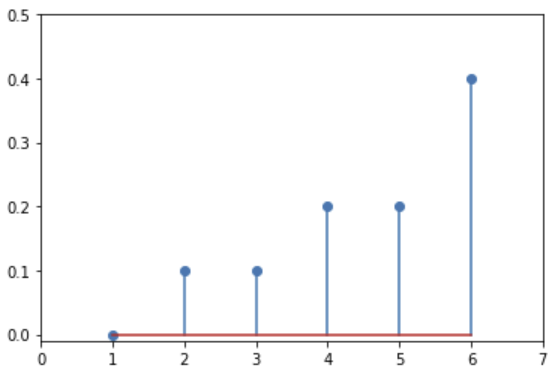
확률 질량 함수
특정 값에서 특정 값에 대한 확률을 나타내는 함수 P(X=x) = f(x)
- 모든 확률은 0보다 큰 성질
- 모든 확률을 합치면 결과값은 1
- a와 b사이의 확률은 a에서 b까지 확률의 합
누적 질량 함수
이산확률변수가 특정 값보다 작거나 같을 확률을 나타내는 함수 P(x≤x) = F(x)
- 함수는 증가함수 그래프
- x값이 -∞면 0, +∞면 1
- a와 b사이의 확률은 F(b)와 F(a) 차이와 같음
연속확률분포
확률변수 X가 실수와 같이 연속적인 값을 취할 때 연속확률변수라 함
정규분포
- 기댓값 : E(X) = m, 분산 V(X) = σ
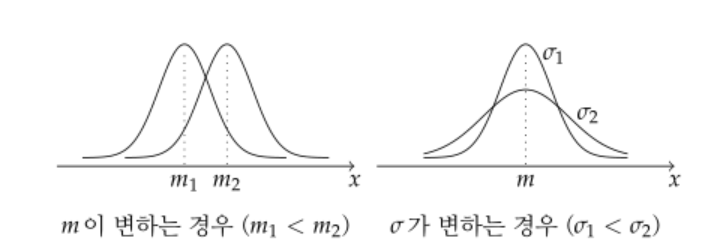
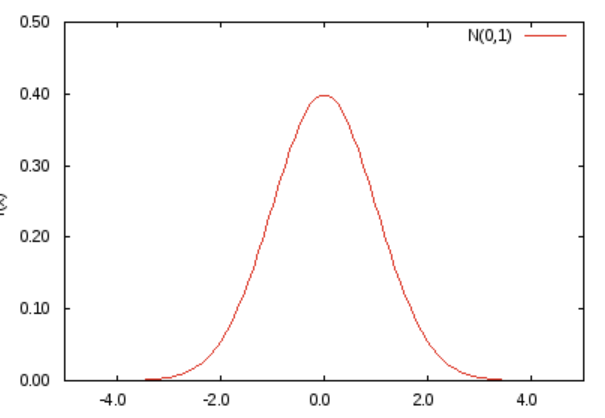
표준정규분포
- 정규분포 함수에서 X를 Z로 정규화한 분포
- 기댓값 E(X) = 0, 분산 V(X) = 1
지수분포
- 지정된 시점으로부터 어떤 사건이 일어날 때까지 걸리는 시간을 측정하는 확률 분포
- 기댓값 E(X) = 1/λ 분산 V(X) = 1/λ²
χ²분포(카이-제곱 분포)
- 표본 통계량이 표본분산일 때의 표준분포
- n개의 서로 독립적인 표준 정규 확률변수를 각각 제곱한 다음 합해서 얻어지는 분포
- 자유도 n이 작을수록 왼쪽으로 치우치는 비대칭적 모양
- 자유도 n≥3부터 단봉 형태, 값이 클수록 정규분포에 가까워짐
- 기댓값 E(X) = n, 분산 V(X) = 2n
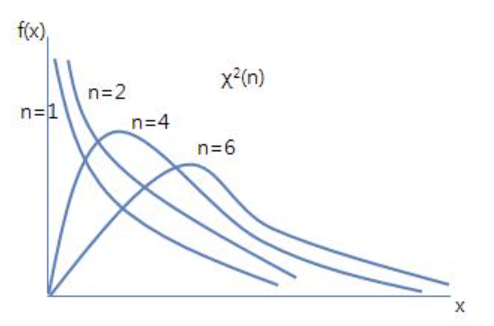
F-분포
- 모집단 분산이 서로 동일하다고 가정되는 두 모집단으로부터 표본 크기가 각각 n1, n2인 독립적인 2개의 표본을 추출하였을 때, 2개의 표본분산 s1², s2²의 비율
- 독립적인 χ² 분포가 있을 때, 두 확률변수의 비
- 기댓값 E(X) = d2/(d2-1), 분산 V(X) = 2d2²(d1+d2-2) / d1(d2-2)²(d2-4)
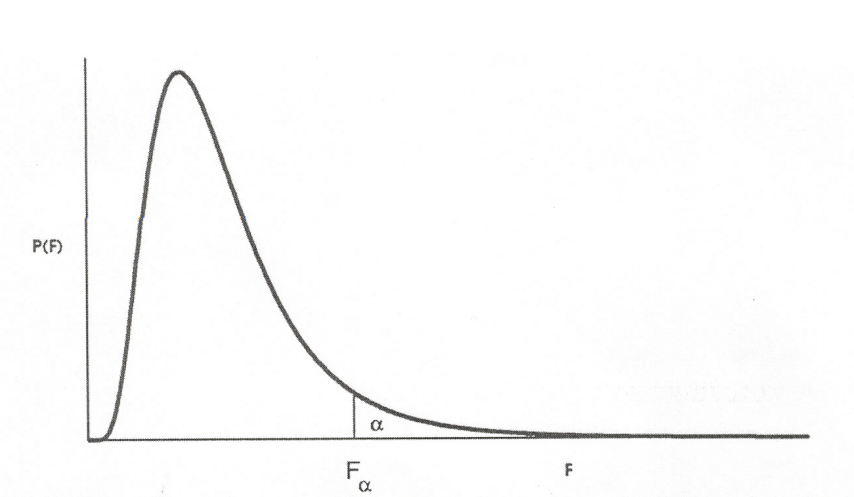
확률밀도함수
연속확률변수의 분포를 나타내는 함수

- 모든 확률은 0보다 커야 함
- 모든 확률을 합치면 1
누적밀도함수

- 함숫값은 증가함수 형태
- x 값이 -∞면 0, +∞면 1
최대우도법
어떤 확률변수에서 표집 한 값들을 토대로 그 확률변수의 모수를 구하는 방법

위 식에 자연로그 ln을 씌워 계산하면

양변을 미분한 값이 0에서 최대우도값을 가진다.

예시
확률밀도 함수가 3, 1, 2, 3, 3이 값을 가질 때 최대우도 추정값을 구해보자
위 공식을 적용하면 ln(L(θ) =lnθ -2θ + lnθ -θ + 3lnθ - 9θ = 5lnθ -12θ
양반을 미분해서 계산하면 12θ = 5이므로 θ=5/12를 구할 수 있다.
표본분포
- 모집단 : 정보를 얻고자 하는 대상이 되는 집단 전체
- 모수 : 모집단의 특성을 나타내는 대푯값
- 표본집합 : 모집단에서 선택된 구성단위의 일부
- 통계량 : 표본에서 얻은 평균이나 표준오차와 같은 값 (이 값을 통해 모수 추정)
※ 기출문제

일치성 : 표본 크기가 증가할수록 좋은 추정값을 제시한다. (답 : 4)
표본조사
- 표본오차 : 모집단을 대표할 수 있는 표본 단위들이 조사대상으로 추출되지 못하기에 발생하는 오차
- 비표본오차 : 표본오차를 제외한 모든 오차로서 조사 과정에서 발생하는 모든 부주의나 실수, 알 수 없는 원인 등 모든 오차를 의미하며 조사대상이 증가하면 오차가 커짐
- 표본편의 : 모수를 작게 또는 크게 할 때 추정한느 것과 같이 표본추출방법에서 기인하는 오차
표본분포 관련 법칙
- 큰 수의 법칙 : 데이터를 많이 뽑을수록(n이 커질수록) 표본평균의 분산은 0에 가까워진다는 법칙
- 중심 극한 정리 : 데이터의 크기가 커지면 그 데이터가 어떠한 형태이든 그 데이터 표본의 분포는 최종적으로 정규분포를 따른다는 법칙
뒤로 이어지는 내용
https://edder773.tistory.com/140
[빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 6
자격증 준비하면서 내가 이해하기 편하게, 다시 보기 좋게 정리하는 빅데이터 분석기사의 내용 (자격증 상세 내용은 아래) https://www.dataq.or.kr/www/sub/a_07.do 데이터자격시험 대용량의 데이터 집합
edder773.tistory.com
'자격증 > 빅데이터 분석 기사' 카테고리의 다른 글
| [빅데이터 분석 기사 필기 3과목] 빅데이터 모델링 정리 - 1 (0) | 2023.04.05 |
|---|---|
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 6 (0) | 2023.04.04 |
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 4 (0) | 2023.04.04 |
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 3 (0) | 2023.04.04 |
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 -2 (0) | 2023.04.04 |




댓글