자격증 준비하면서 내가 이해하기 편하게, 다시 보기 좋게 정리하는 빅데이터 분석기사의 내용 (자격증 상세 내용은 아래)
https://www.dataq.or.kr/www/sub/a_07.do
데이터자격시험
대용량의 데이터 집합으로부터 유용한 정보를 찾고 결과를 예측하기 위해 목적에 따라 분석기술과 방법론을 기반으로 정형/비정형 대용량 데이터를 구축, 탐색, 분석하고 시각화를 수행하는 업
www.dataq.or.kr
2과목인 빅데이터 분석 기획을 정리한 내용
추론통계
- 모집단의 표본을 가지고 모집단의 특성을 추정하고, 결과의 신뢰성을 검정하는 통계적 방법
- 표본 개수가 많을수록 표본 오차 감소
- 표본의 데이터인 일부의 데이터를 이용하여 모집단을 추정하므로 어느 정도 오차 존재
※ 기출문제

통계적 추론 또는 통계적 추측은 모집단에 대한 어떤 미지의 양상을 알기 위해 통계학을 이용하여 추측하는 과정을 지칭하며 통계학의 한 부분으로서 추론 통계학이라고 불린다. 이것은 기술 통계학과 구별되는 개념이다.
점 추정
- 표본의 정보로부터 모집단의 모수를 하나의 값으로 추정하는 기법
- 신뢰도를 나타낼 수 없는 단점이 있어 구간 추정을 주로 사용
- 표본평균, 표본분산, 중위수, 최빈수 사용
점 추정 조건
- 불편성(불편의성) : 추정량의 기댓값이 모집단의 모수와 차이가 없다는 특성 (불편 추정량은 모수 중심 분포)
- 효율성 : 추정량의 분산이 작을수록 좋다는 특성 (항상 1 이하이며 1일 경우 최대효율 추정량)
- 일치성 : 표본의 크기가 아주 많이 커지면, 추정량이 모수와 거의 같아진다는 특성(일치 추정량 사용)
- 충족성(충분성) : 추정량은 모수에 대하여 많은 정보를 제공할수록 좋다는 특성(충족 추정량 사용)
※ 기출문제

구간 추정은 점추정에 오차의 개념을 도입하여 모수가 포함되는 확률변수구간을 어떤 신뢰성 아래 추정하는 것이다. (답 : 4)
표준 오차
- 표본 평균의 표준오차

- 표본비율의 표준오차

구간 추정
추정값에 대한 신뢰도를 제시하면서 범위로 모수를 추정하는 방법
- 신뢰 수준
- 추정값이 존재하는 구간에 모수가 포함될 확률
- 100 × (1-α)%로 계산
- 주로 90%, 95%, 99% 신뢰 수준 사용
- 신뢰구간
- 신뢰 수준을 기준으로 추정된 통계적으로 유의미한 모수 범위
- 신뢰구간은 왼쪽과 오른쪽을 다루므로 α를 반으로 나눈 α/2 많이 사용
모평균 추정
모분산이 알려져 있는 경우
- 검정통계량

- 모평균 추정

모분산이 알려져 있지 않은 경우(대표본의 크기에 따라 달라짐)
- 검정통계량

- 모평균 추정(대표본 n < 30)

- 모평균 추정(대표본 ≥ 30)

두 모평균 차이의 추정
모분산이 알려져 있는 경우
- 검정통계량

- 모평균 차이 추정

모분산이 알려져 있지 않은 경우 (대표본 ≥30)
- 검정통계량
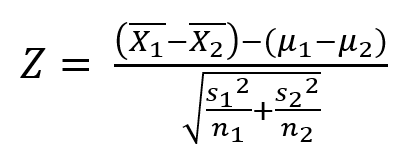
- 모평균 차이 추정
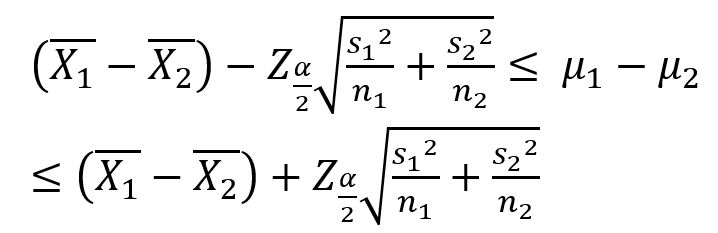
두 모분산이 같고 소표본일 경우
- 검정통계량
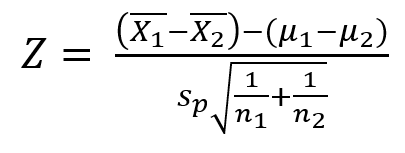
- 모평균 차이 추정
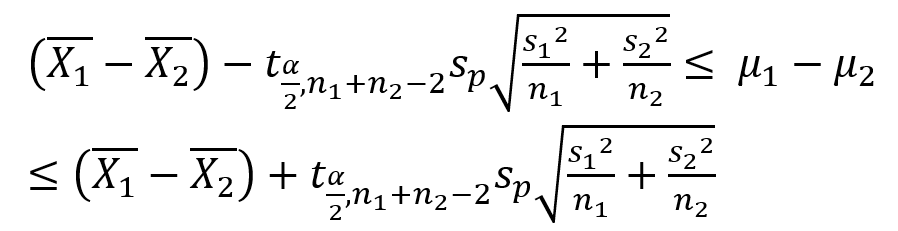
모비율 추정
단일 모비율 추정
- 검정통계량
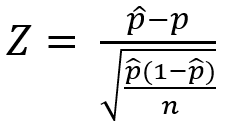
- 단일 모비율 추정
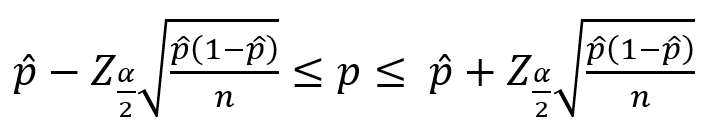
두 모비율 차이의 추정
- 검정통계량
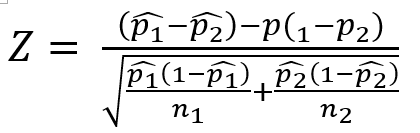
- 단일 모비율 추정
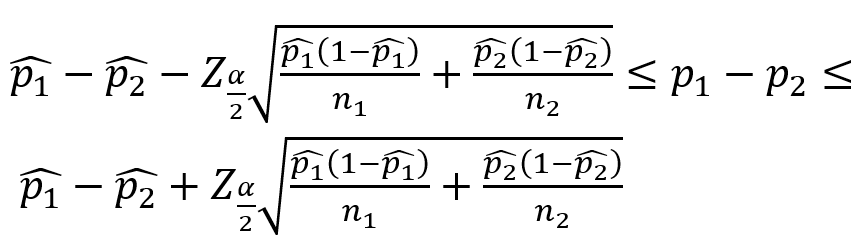
표본 크기 결정
- 모분산을 알 경우 표본의 크기
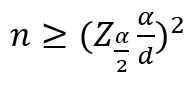
- 모분산을 모르는 경우 표본의 크기

- 모비율이 알려져 있을 경우 표본의 크기
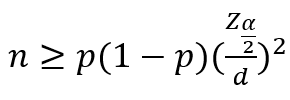
- 표본비율이 알려져 있을 경우 표본의 크기
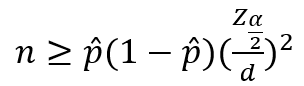
- 모비율과 표본비율이 알려져 있지 않을 경우 표본의 크기
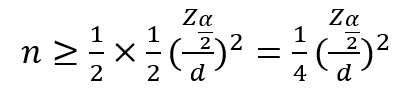
비모수 통계특징
평균이나 분산 같은 모집단의 분포에 대한 모수성을 가정하지 않고 분석하는 통계적 방법
- 장점
- 모집단의 분포에 대한 가정의 불만족으로 인한 오류 가능성 낮음
- 모수적 방법에 비해 통계량의 계산이 간편하고 직관적으로 이해하기 쉬움
- 모집단의 분포에 무관하게 사용가능
- 이상값으로 인한 영향 적음
- 단점
- 모수 통계로 검정이 가능한 데이터를 비모수 통계를 이용하면 효율성 떨어짐
- 검정통계량의 신뢰성 부족
- 자료 수가 많을 경우 모수적 통계에 비해 계산 절차 복잡
단일 표본 부호검정
차이의 크기는 무시하고 차이의 부호만을 이용한 중위수의 위치에 대한 검정 방법
- 표본 추출
- 모집단에서 연속적인 표본을 추출
- 가정된 중위수와 같은 표본을 제외 후 남은 표본의 수가 n개 일 때, 남은 표본을 X1, X2…, Xn이라 정의
- 검정 통계량
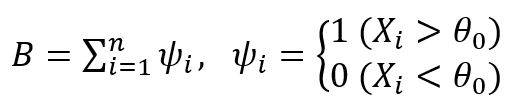
- 유의 수준 α에 대한 기각역
- b(α, n,½)는 표본의 크기 n, 성공확률인 베르누이의 이항분포 B(n, ½)의 상위 100α, 백분위수로 P(B ≥ b(α, n, ½))을 만족하는 값
윌콕슨 부호 순위 검정 절차
- 가설 설정
- 모집단에서 n개의 연속적인 표본 X1, X2, … , Xn을 추출하였을 때, 귀무가설(H0)과 대립가설(H1) 설정
- H0 : θ = θ, H1 : θ (>, <, ≠) θ0
- 표본과 중위수 간의 차이 계산
- Yi = Xi - θ0
- Ri+ 계산
- |Yi|를 구하고 Yi의 가장 낮은 절댓값을 1부터 시작하여가장 높은 값을 n으로 순위를 부여하여 Ri+를 구함
- 검정 통계량 계산
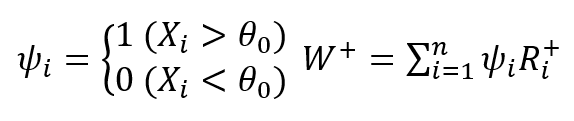
- 유의 수준 α에 대한 기각역
- 귀무가설, 대립가설에 따른 기각역을 각각 구함
두 표본 검정 윌콕슨 순위 합검정 절차
- 1. 가설 설정
- 귀무가설(H0)과 대립가설(H1) 설정
- H0 Δ= 0, H1 =Δ(>, <, ≠) 0
- 2. 순위 부여
- N(m+n) 개의 혼합 샘플에서 Xi와 Yj의 순위를 부여
- 3. 순위 계산
- N개의 혼합 샘플에서 Yj의 순위인 Rj 계산
- 4. 검정통계량 계산
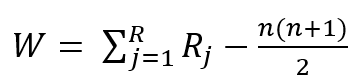
- 5. 유의 수준 α에 대한 기각역
- 귀무가설, 대립가설에 따른 기각역을 각각 구함
- 혼합 표본에 동점이 있을 경우 W는 동점 간 평균 순위 사용
분산 분석 - 크루스칼 왈리스 검정
- 세 집단 이상 분포를 비교하는 검정 방법
- one-way-ANOVA와 같은 목적으로 사용
- 각 그룹의 표본 수는 다를 수 있음
크루스칼 왈리스 검정 절차
- 1. 가설 설정
- 귀무가설(H0)과 대립가설(H1) 설정
- H0 각 그룹 간의 중위수는 같음, H1 : 적어도 1개 그룹의 중위수는 다름
- 2. 순위 부여
- 혼합 표본 n개를 크기순으로 나열하여 1~n까지 순위를 부여
- 3. 순위 계산
- 각 그룹의 순위 합, 평균 순위, 그리고 총 평균 순위 계산
- 4. 검정통계량 계산
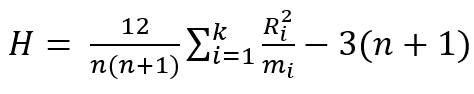
- 5. 유의 수준 α에 대한 기각역
- H ≥ h(α, k, (1, 2, …, m))이면 H0를 기각
- h(α, k, (1, 2, …, m))은 H의 상위 100α 백분위수로 P(H ≥ h(α, k, (1, 2, …, m)))을 만족하는 값
런 검정
- 두 개의 값을 가지는 연속적인 측정값들이 어떤 패턴이나 영향이 없이 임의적으로 나타난 것인지를 검정하는 방법
- 이분화된 자료가 아닌 경우는 이분화된 자료로 변환시켜야 함
- 평균, 중위수, 최빈수, 사용자가 정한 기준값을 이용하여 이분화
런 검정 절차
- 1. 가설 설정
- 귀무가설(H0)과 대립가설(H1) 설정
- H0 : 연속적인 측정값들이 임의적, H1 : 연속적인 측정값들이 임의적이 아님
- 2. 검정 통계량
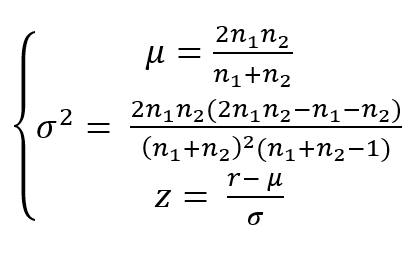
- 3. 기각역
- z의 p-값이 하한 기각역보다 작거나(같은 경우 포함) 상한 기각역보다 큰 경우 귀무가설을 기각)
가설 검정
- 모집단에 대한 통계적 가설을 세우고 표본을 추출한 다음, 그 표본을 통해 얻은 정보를 이용하여 통계적 가설의 진위를 판단하는 과정
- 귀무가설(H0) : 현재까지 주장되어 온 것이나 기존과 비교하여 변화 혹은 차이가 없음을 나타내는 가설
- 대립가설(H1) : 표본을 통해 확실한 근거를 가지고 입증하고자 하는 가설
가설 검정 절차
- 가설 설정 : 귀무가설과 대립가설 설정 및 양측 검정, 좌우측 검정 결정
- 유의 수준 설정 ; 유의 수준 α 설정 (보통 0.05)
- 검정통계량 계산 (p-값 산출) : t-값, Z-값 등의 검정통계량과 검정통계량에 따른 p-값 산출
- 검정통계량> 임계값 / p-값 < 유의 수준 : 검정통계량의 값과 임계값을 비교하거나 p-값과 유의 수준 비교
- 의사 결정 : 귀무가설의 채택 및 기각
가설검정 방법
- 양측 검정
- 모수 혹은 모수들의 함수에 대해 표본자료를 바탕으로 모수가 특정 값과 통계적으로 같은지 여부를 판단
- 귀무가설 H0 : θ = θ0, 대립 가설 H1 : θ ≠ θ0으로 설정
- 단측 검정
- 모수 혹은 모수들의 함수에 대해 표본 자료를 바탕으로 모수가 특정 값과 통계적으로 큰지 작은지 여부를 판단
- 좌측 검정일 경우 귀무 가설 H0 : θ = θ0, 대립 가설 H1 : θ < θ0으로 설정
- 우측 검정일 경우 귀무 가설 H0 : θ = θ0, 대립 가설 H1 : θ > θ0으로 설정
가설검정 오류
일반적으로 1종 오류의 영향 > 2종 오류의 영향
- 제1종 오류 : 귀무가설이 참인데 잘못하여 이를 기각하게 되는 오류
- 유의 수준 : 제1종 오류를 범할 최대 허용 확률을 의미(α)
- 신뢰 수준 : 귀무가설이 참일 때 이를 참이라고 판단하는 확률(1-α)
- 제2종 오류 : 귀무가설이 거짓인데 잘못하여 이를 채택하게 되는 요류
- 베타 수준 : 제 2종 오류를 범할 최대 허용 확률을 의미(β)
- 검정력 : 귀무가설이 참이 아닌 경우 이를 기각할 수 있는 확률 (1-β)
※ 기출문제

제3종 오류는 존재하지 않는다 (답 : 3)
p-값 유의 확률
p-값은 귀무가설이 참이라는 전제하에 실제 표본에서 구한 표본 통계량의 값보다 더 극단적이 값이 나올 확률
- 귀무가설 채택 : p-값 > 유의 수준(α)
- 귀무가설 기각 : p-값 < 유의 수준(α)
임계값
주어진 유의 수준을 검정통계량의 값으로 환산한 값으로서 귀무가설을 채택 또는 기각하는 기준
- 귀무가설 채택 : 임계값 > 검정통계량
- 귀무가설 기각 : 임계값 < 검정통계량
※ 기출문제

임계치 : 주어진 유의 수준 α에서 귀무가설의 채택과 기각에 관련된 의사 결정을 할 때, 그 기준이 되는 점
※ 기타 기출문제

군집분석 : 변수 또는 개체들이 속한 모집단 또는 범주에 대한 사전 정보가 없는 경우에 관측값들 사이의 거리(또는 유사성)를 이용하여 변수 또는 개체들을 자연스럽게 몇 개의 그룹 또는 군집(cluster)으로 나누는 분석법으로 정의한다. (답 : 4)

단일용인변수 (독립변수)에 의해 종속변수에 대한 평균치의 차이를 검정하는데 이용한다. (답 : 2)

자유도가 클수록 정규분포에 모양이 수렴된다.
자유도가 1보다 클 때만 스튜던트 t 분포에서 기댓값은 0이다 스튜던트 t분포는 정규분포의 평균 측정 시 주로 사용하는 분포이다.
분포의 모양은 Z-분포와 유사하다. 종 모양으로서 t= 0에 대하여 대칭을 이루는데 t-곡선의 모양을 결정하는 것은 자유도이다. (답 : 1)

이상치가 비 무작위성을 가지고 나타나게 되면 데이터의 정상성 감소를 초래하며 이는 데이터 자체의 신뢰성 저하로 연결될 가능성이 있다. 정상성이 높아지면 데이터의 신뢰도가 높아진다. (답 : 1)

첨도, 왜도는 데이터의 분포모양에 해당된다. 중앙값은 전체변수의 범위에서 가운데가 아니라 관찰된 변수들 중의 가운데 값이므로 이상값의 영향을 받지 않는다 (답 : 3)

특정 상황에만 의미성 부여가 아닌 보편적이고 전 데이터구간에 대표성을 가지는 변수생성을 위해서 노력해야 한다.’는 파생변수의 생성 및 처리 시의 유의점 설명이다. (답 : 1)

다수 클래스 데이터에서 일부만 사용하는 방법은 언더샘플링, 소수 클래스 데이터를 증가시키는 것은 오버샘플링이다. (답 : 1)

질적자료 : 정성적 자료라고도 하며 자료를 범주의 형태로 분류한다. 분류의 편리상 부여된 수치의 크기자체에는 의미를 부여하지 않는 자료이며 명목자료, 서열자료 등이 질적자료로 분류된다. (답 : 2)

수치자료의 정의 : 수치의 크기에 의미를 부여할 수 있는 자료를 나타내며 구간 자료, 비율 자료가 여기에 속한다. (답 : 2)

서열자료는 질적자료이다 (답 : 2)

서로 다른 관찰치 간의 오차항은 상관이 없다(오차항은 서로독립이며 공분산은 0) (답 : 3)

보기 4는 군집분석 중 비계층적 방법을 나타낸 내용이다. (답 : 4)

원자료 : 표본에서 조사된 최초의 자료를 이야기한다. (답 : 4)

회귀분석의 경우 하나의 반응변수를 여러 개의 설명변수로 설명하고자 할 때, 가장 설명력이 높은 변수들의 선형결합을 찾아 이들 사이의 인과관계를 생각하는 반면에 정준분석에서는 이와 같은 인과성이 없다. (답 : 4)
뒤로 이어지는 3과목
https://edder773.tistory.com/142
[빅데이터 분석 기사 필기 3과목] 빅데이터 모델링 정리 - 1
자격증 준비하면서 내가 이해하기 편하게, 다시 보기 좋게 정리하는 빅데이터 분석기사의 내용 (자격증 상세 내용은 아래) https://www.dataq.or.kr/www/sub/a_07.do 데이터자격시험 대용량의 데이터 집합
edder773.tistory.com
'자격증 > 빅데이터 분석 기사' 카테고리의 다른 글
| [빅데이터 분석 기사 필기 3과목] 빅데이터 모델링 정리 - 2 (0) | 2023.04.05 |
|---|---|
| [빅데이터 분석 기사 필기 3과목] 빅데이터 모델링 정리 - 1 (0) | 2023.04.05 |
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 5 (0) | 2023.04.04 |
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 4 (0) | 2023.04.04 |
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 3 (0) | 2023.04.04 |




댓글