자격증 준비하면서 내가 이해하기 편하게, 다시 보기 좋게 정리하는 빅데이터 분석기사의 내용 (자격증 상세 내용은 아래)
https://www.dataq.or.kr/www/sub/a_07.do
데이터자격시험
대용량의 데이터 집합으로부터 유용한 정보를 찾고 결과를 예측하기 위해 목적에 따라 분석기술과 방법론을 기반으로 정형/비정형 대용량 데이터를 구축, 탐색, 분석하고 시각화를 수행하는 업
www.dataq.or.kr
3과목인 빅데이터 모델링을 정리한 내용
데이터 분할
데이터를 훈련 · 검증 · 평가 데이터로 분할하는 작업
- 훈련 데이터 : 알고리즘의 학습을 위한 데이터
- 검증 데이터 : 트레이닝 세트로 학습된 모델의 예측/분류 정확도를 계산하기 위한 데이터
- 평가 데이터 : 학습된 모델의 성느이 어느 정도 만족스러운지 평가하기 위한 실제 데이터
- 검증 데이터를 사용해 모형의 학습 과정에서 제대로 학습되었는지 중간에 검증 실시 가능
- Early Stopping 사용 가능
회귀 분석
- 독립변수와 종속변수 간에 선형적인 관계를 도출해서 하나 이상의 독립변수들이 종속변수에 미치는 영향을 분석하고, 독립변수를 통해 종속변수를 예측하는 분석 기법
- 변수들 사이의 인과관계를 밝히고 모형을 적합하여 관심 있는 변수를 예측하거나 추론하기 위한 분석 방법
회귀 모형 가정
- 선형성
- 독립변수와 종속변수가 선형적이어야 한다는 특성
- 독립변수의 변화에 따라 종속변수도 일정 크기로 변화
- 독립성
- 단순선형 회귀 분석에서는 잔차와 독립변수의 값이 서로 독립적이어야 한다는 특성
- 다중선형 회귀 분석에서는 독립변수 간 상관성이 없이 독립적이어야 함
- 통계량으로는 더빈-왓슨 검정을 통해 가능
- 등분산성
- 잔차의 분산이 독립변수와 무관하게 일정해야 한다는 특성
- 잔차가 고르게 분포되어야 함
- 비상관성
- 관측치와 잔차는 서로 사관이 없어야 한다는 특성
- 잔차끼리 서로 독립이면 비상관성이 있다고 판단
- 정상성
- 잔차항이 정규분포의 형태를 이뤄야 한다는 특성
- Q-Q Plot에서는 잔차가 대각 방향의 직선의 형태를 띠면 잔차는 정규분포를 따른다고 할 수 있음
- 통계량으로는 샤피로-윌크 검정, 콜모고로프-스미르노프 검정 등을 통해 확인 가능
회귀 모형 검증
- 통계적으로 유의미한지?
- F-통계량을 통해 확인
- 유의 수준 5% 하에서 F- 통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의미하다고 볼 수 있음
- 회귀계수들이 유의미한지?
- t-통계량을 통해 각 독립변수가 종속변수에 미치는 영향을 파악
- 해당 계수의 t-통계량과 p-값 또는 이들의 신뢰구간 확인
- 회귀 모형이 얼마나 설명력이 있는가?
- 회귀식 자체의 유의성 확인
- 모형의 설명력은 결정계수(R²)로 확인
- 결정계수는 전체 변동 중 회귀 모형에 의해 설명되는 변동의 비율로 표본에 의해 추정된 회귀식이 주어진 자료를 얼마나 잘 설명하는가를 보여주는 값
- 결정계수는 0~1 값을 가지며, 높은 값을 가질수록 추정된 회귀식의 설명력이 높음
- 회귀 모형이 데이터를 잘 적합하는가?
- 잔차를 그래프로 그리고 회귀진단
- 데이터가 가정을 만족하는가?
- 선형성, 독립성, 등분산성, 비상관성, 정상성 가정을 만족시켜야 함
회귀 분석 유형
- 단순 선형 회귀 : 독립변수가 1개이며, 종속변수와의 관계가 직선
- 다중 선형 회귀 : 독립변수가 K개이며, 종속변수와의 관계가 선형(1차 함수)
- 다항 회귀 : 독립변수와 종속변수와의 관계가 1차 함수 이상인 관계(단, 독립변수가 1개일 경우에는 2차 함수 이상)
- 곡선 회귀 : 독립변수가 1개이며, 종속변수와의 관계가 곡선
- 로지스틱회귀 : 종속변수가 범주형(2진 변수)인 경우 적용
- 비선형 회귀 : 회귀식의 모양이 미지의 모수들의 선형관계로 이뤄져 있지 않은 모형
단순선형 회귀 분석
- 독립변수와 종속변수가 각각 1개이며 오차항이 있는 선형관계로 이루어짐
- 회귀 계수는 최소제곱법을 사용하여 추정함
- y = β0 + β1xi
회귀 분석 검정
- 회귀 계수 검정
- 회귀계수가 0이면 입력변수와 출력변수는 인과관계가 없음
- 결정 계수
- 전체데이터를 회귀 모형이 얼마나 잘 설명하고 있는지를 보여주는 지표로 회귀선의 정확도를 평가
- 전체 제곱합에서 회귀 제곱합의 비율
- 회귀직선의 적합도 검토
- 결정계수를 통해 추정된 회귀식이 얼마나 타당하는지 검토
- 결정계수가 1에 가까울수록 회귀 모형이 자룔 잘 설명함
다중 선형 회귀 분석
- 모형의 통계적 유의성
- 통계적 유의성은 F-통계량으로 확인
- 유의 수준 5% 하에서 F-통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의미
- F-통계량이 크면 p-값이 0.05보다 작아지고 귀무가설을 기각하므로 모형이 유의
- 다중선형 회귀 분석 검정
- 회귀 계수의 유의성 : 회귀계수 유의성 검토와 같이 t-통계량을 통해 확인
- 결정계수 : 전체 데이터의 회귀 모형이 얼마나 잘 설명하고 있는지를 보여주는 지표
- 수정된 결정계수 : 설명력이 떨어지는 독립변수가 추가될 때는 감소하는 성질을 가지고 있으므로 모형 선택의 관점에서 이용
- 모형의 적합성 : 모형이 적합한지 잔차와 종속변수의 산점도로 확인
- 다중공선성 : 회귀 분석에서 독립변수들 간에 강한 상관관계가 나타나는 문제 (데이터 분석 시 부정적 영향)
※ 기출문제

잔차들의 분산이 일정해야 하며 1이 될 필요는 없다. (답 : 3)

다중공선성 진단 → 회귀계수 유의성 확인 → 수정된 결정계수 확인 → 모형의 적합도 평가(답 : 4)
최적 회귀방정식의 선택
- 전진 선택법 : 절편만 있는 상수 모형부터 시작해 중요하다고 생각되는 독립변수를 차례로 모형에 추가하는 방식
- 후진 소거법 : 독립변수 후보 모두를 포함한 모형에서 출발해 제곱합의 기준으로 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 더 이상 유의하지 않은 변수가 없을 때까지 독립변수들을 제거하고 이때의 모형을 선택하는 방법
- 단계적 방법 : 변수를 추가하면서 새롭게 추가된 변수에 기인해 기존 변수가 그 중요도가 약화되면 해당 변수를 제거하는 단계별 추가 또는 제거되는 변수의 여부를 검토해 더 이상 없을 때 중단하는 방법
벌점화된 선택기준
- AIC
- AIC = -2ln(L) + 2p
- 값이 낮을수록 모형 적합도 높음
- 적합도를 높이기 위해 여러 불필요한 매개변수를 사용할 수도 있음
- 표본이 커질수록 부정확해짐
- BIC
- BIC = -2ln(L) + pln(n)
- 표본 크기가 커질수록 pln(n)도 함께 커짐
- 커질수록 복잡한 모형을 더 강하게 처벌
선형 회귀 분석 코드 해석
- Im() : 선형 회귀 모형을 수행하는 함수
- Residual : 예측하고자 하는 변수의 실제값과 회귀 분석으로 얻어진 값 사이에서 표준 오차로 인해 발생한 차이
- Coefficients : 회귀 모형에서 사용되는 회귀계수
- Significance starts() : 계산된 p-값에 따라 별표로 나타내는 중요도 수준 (높은 중요도 : ***, 낮은 중요도 : *)
- Multiple R-squared : 결정계수(R²)로 모델에 의하여 해석되는 예측의 변동량으로 모델의 적합성을 평가하는 척도
- Adjusted R-squared : 수정된 결정계수
- F-statistic : F-통계량
- DF : 샘플에 포함된 관측치의 개수와 모델에 사용된 변수 개수와의 차이
- p-value : 귀무가설이 참이라는 가정에 따라 주어진 표본 데이터를 희소 또는 극한값으로 얻을 확률값
로지스틱 회귀 분석
- 독립변수가 수치형이고 반응변수가 범주형인 경우 적용되는 회귀 분석 모형
- 새로운 설명변수의 값이 주어질 때 반응변수의 각범주에 속할 확률이 얼마인지를 추정하여 추정 확률을 기준치에 따라 분류하는 목적으로 사용
- 0~1 범위를 벗어나는 단순 선형회귀를 사용하면 예측의 정확도가 떨어지기에 사용
로지스틱 회귀 분석 원리
- 오즈(Odds) : 특정 사건이 발생할 확률과 그 사건이 발생하지 않을 확률의 비 = p / 1-p
- 로짓(Logit) 변환 : 오즈에 로그를 취한 함수로 입력값의 범위가 0~1일 때 출력 범위를 -∞ ~ ∞로 조정 = log(Odds)
- 시그모이드 함수 : S자형 곡선을 갖는 수학 함수로 로짓 함수에 역함수를 취하면 얻을 수 있음 = 1 / 1+e^-x
※ 기출문제

종속변수 : 범주형 변수, 분포 : 이항분포 (답 : 3)
의사결정나무
- 의사결정 규칙을 나무구조로 나타내어 전체 자료를 몇 개의 소집단으로 분류하거나 예측하는 분석 방법
- 분석 대상을 분류함수를 활용하여 의사결정 규칙으로 이루어진 나무 모양으로 그리는 기법
의사결정나무 구성요소
- 부모 마디 : 주어진 마디의 상위에 있는 마디
- 자식 마디 : 하나의 마디로부터 분리되어 나간 2개 이상의 마디들
- 뿌리 마디 : 시작되는 마디로 전체 자료를 포함
- 끝 마디 : 잎 노드라고도 불리며, 자식 마디가 없는 마디
- 중간 마디 : 부모 마디와 자식 마디가 모두 있는 마디
- 가지 : 뿌리 마디로부터 끝마디까지 연결된 마디들
- 깊이 : 뿌리 마디부터 끝마디까지의 중간 마디들의 수
※ 기출문제

깊이(depth)는 가지를 이루는 마디의 개수이다. (답 : 4)
의사결정나무 분석 과정
- 의사 결정 나무 성장
- 목표변수와 관계가 있는 설명 변수를 추가하고 분석목적과 자료구에 따라 적절한 분리규칙을 찾아 나무를 성장시키는 과정
- 정지 규칙을 만족하면 중단
- 가지치기
- 분류 오류를 크게 할 위험이 높거나 부적절한 추론 규칙을 가진 가지 또는 불필요한 가지를 제거
- 타당성 평가
- 이익 도표, 위험 도표, 또는 평가 데이터를 이용하여 교차 타당성 등을 이용한 평가 수행
- 해석 및 예측
- 구축된 의사결정나무 모형을 해석하고 분류 및 예측 모형을 설정하여 데이터의 분류 및 예측에 활용하는 단계
의사결정나무 분리 기준
- 하나의 부모 마디로부터 자식 마디들이 형성될 때, 입력변수의 선택과 범주의 병합이 이루어질 기준을 의미
- 목표변수의 분포를 구별하는 정도로를 순수도 또는 불순도에 의해서 측정
- 목표 변수가 이산형인 경우 분류나무, 연속형인 경우 회귀나무로 구분
분류나무 분리 기준
- 카이제곱 통계량의 p-값 : p-값이 가장 작은 예측변수와 그 당시의 최적 분리를 통해서 자식 마디 형성
- 지니 지수 : 불순도를 측정하는 하나의 지수로서 지니 지수를 가장 감소시켜 주는 예측변수와 그 당시의 최적 분리를 통해서 자식 마디 선택
- 엔트로피 지수 : 엔트로피 지수가 가장 작은 예측변수와 그 당시의 최적 분리를 통해서 자식 마디 형성
※ 기출문제

답 : 3
회귀나무 분리 기준
- 분산 분석에서 F-통계량 : p-값이 가장 작은 예측변수와 그 당시의 최적 분리를 통해서 자식 마디 형성
- 분산의 감소량 : 예측 오차를 최소화하는 것과 같은 기준으로 분산의 감소량을 최대화하는 기준의 최적 분리를 통해서 자식 마디형성
정지 규칙
- 더 이상 분리가 일어나지 않고 현재의 마디가 끝마디가 되도록 하는 규칙
- 의사결정나무의 깊이를 지정, 끝마디의 레코드 수의 최소 개수를 지정
※ 기출문제

답 : 4
가지치기
- 너무 큰 나무는 모형은 훈련 데이터에 대한 성능은 좋지만 실제 데이터에 성능이 떨어지는 현상인 과대 적합 발생
- 너무 작은 나무 모형은 적정 수준의 학습이 부족하여 실제 성능이 떨어지는 과소 적합 발생
- 일반적으로 마디에 속하는 자료가 일정 수 이하일 때 분할을 멈추고 비용-복잡도 가지치기를 활용하여 성장시킨 나무에 대한 가지치기 진행
불순도의 척도
- 카이제곱 통계량 : 데이터 분포와 사용자가 선택한 기대 또는 가정된 분포 사이의 차이를 나타내는 측정값
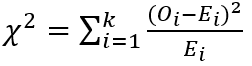
- 지니 지수 : 노드의 불순도를 나타내는 값으로 값이 클수록 이질적이며 순수도가 낮음
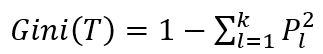
- 엔트로피 지수
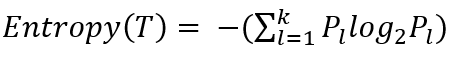
다음과 같은 데이터에서 카이제곱 통계량 & 지니지수 & 엔트로피 지수 구하기
| A | B | 합계 | |
| X | 32 | 48 | 80 |
| Y | 178 | 42 | 220 |
| 합계 | 210 | 90 | 300 |
- 기대도수 구하기
| A | B | |
| X | 80*210/300 = 56 | 80*90/300 = 24 |
| Y | 220*210/300=154 | 220*90/300 = 66 |
- 카이제곱 통계량 구하기
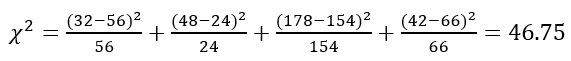
- 지니 지수 구하기
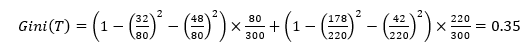
- 엔트로피 지수 구하기
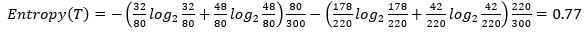
※ 기출문제

2번은 카이제곱검정에 대한 설명이다. (답 : 2)
뒤로 이어지는 내용
https://edder773.tistory.com/144
[빅데이터 분석 기사 필기 3과목] 빅데이터 모델링 정리 - 3
자격증 준비하면서 내가 이해하기 편하게, 다시 보기 좋게 정리하는 빅데이터 분석기사의 내용 (자격증 상세 내용은 아래) https://www.dataq.or.kr/www/sub/a_07.do 데이터자격시험 대용량의 데이터 집합
edder773.tistory.com
'자격증 > 빅데이터 분석 기사' 카테고리의 다른 글
| [빅데이터 분석 기사 필기 3과목] 빅데이터 모델링 정리 - 4 (0) | 2023.04.06 |
|---|---|
| [빅데이터 분석 기사 필기 3과목] 빅데이터 모델링 정리 - 3 (0) | 2023.04.05 |
| [빅데이터 분석 기사 필기 3과목] 빅데이터 모델링 정리 - 1 (0) | 2023.04.05 |
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 6 (0) | 2023.04.04 |
| [빅데이터 분석 기사 필기 2과목] 빅데이터 탐색 정리 - 5 (0) | 2023.04.04 |




댓글